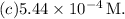Final answer:
The concentration of hydronium ion
 in the solution is approximately
in the solution is approximately
 Therefore, the correct answer is option
Therefore, the correct answer is option
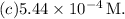
Step-by-step explanation:
To determine the concentration of hydronium ion
 in the solution, we can use the ionization constant
in the solution, we can use the ionization constant
 of lactic acid. The balanced chemical equation for the ionization of lactic acid is:
of lactic acid. The balanced chemical equation for the ionization of lactic acid is:
![\[ \text{CH}_3\text{CH(OH)CO}_2\text{H} \rightleftharpoons \text{CH}_3\text{CH(OH)CO}_2^- + \text{H}_3\text{O}^+ \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/m1czcfabi8pnvqnrn2710241wqlsdrj7yw.png)
Given that the ionization constant
 is
is
 , we can set up an ICE (initial, change, equilibrium) table for the ionization reaction:
, we can set up an ICE (initial, change, equilibrium) table for the ionization reaction:
![\[\begin{array}{cccc}& \text{CH}_3\text{CH(OH)CO}_2\text{H} & \rightleftharpoons & \text{CH}_3\text{CH(OH)CO}_2^- & + & \text{H}_3\text{O}^+ \\\text{Initial (M)} & x & & 0 & & 0 \\\text{Change (M)} & -x & & +x & & +x \\\text{Equilibrium (M)} & x & & x & & x \\\end{array}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/qdjpjz7tgl7vey7mcldtf3e1ze33xluzox.png)
The ionization constant
 is given by the expression:
is given by the expression:
![\[ K_a = \frac{\text{[CH}_3\text{CH(OH)CO}_2^-]\text{[H}_3\text{O}^+]}{\text{[CH}_3\text{CH(OH)CO}_2\text{H}]} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/ftxgcl0d14mt44irhtv6sphw4sfagz0b3x.png)
Substitute the equilibrium concentrations into the
 expression:
expression:
![\[ 1.36 * 10^(-4) = (x * x)/(0.020 - x) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/bia4v19sbw8ag9qqgezb19atr08g2wfngh.png)
Since
 is expected to be small compared to 0.020, we can approximate
is expected to be small compared to 0.020, we can approximate
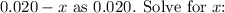
![\[ x^2 = 1.36 * 10^(-4) * 0.020 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/szd4vrhof6otnowlqoy50z23kvmeak4h91.png)
![\[ x = \sqrt{1.36 * 10^(-4) * 0.020} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/wnxmohngmhjh0ghstypn6ux7cl9rgtck6a.png)
![\[ x \approx 5.44 * 10^(-4) \, \text{M} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/4pljs4bizt83bl5aoz3s1zklf5iaxv0ey0.png)
So, the concentration of hydronium ion
 in the solution is approximately
in the solution is approximately
 Therefore, the correct answer is option
Therefore, the correct answer is option