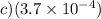Final answer:
The pH of a 0.23-M solution of HF is 1.92. The value of the acid dissociation constant (Kₐ) for HF can be determined using the relationship between pH and Kₐ. By substituting the given concentration and pH values into the appropriate formulas, we find that the value of Kₐ for HF is approximately (3.7 × 10⁻4).
The correct answer is:
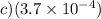 .
.
Step-by-step explanation:
The pH of a solution is related to the concentration of hydronium ions
 through the formula:
through the formula:
![\[ \text{pH} = -\log[\text{H}_3O^+] \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/yp2xe9l70vn8fwp7ht3wt8oeqfrirqcx2m.png)
In the case of hydrofluoric acid (HF), it partially ionizes in water according to the equation:
![\[ \text{HF} \rightleftharpoons \text{H}^+ + \text{F}^- \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/vh1bl82keyyermxgyo1uq2owrva9vmot8d.png)
The ionization constant
 for HF is given by the expression:
for HF is given by the expression:
![\[ K_a = \frac{[\text{H}^+][\text{F}^-]}{[\text{HF}]} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/urdck4ygurvkmn4h8u9vtluzonmbrelykb.png)
Given that the pH of the solution is 1.92, we can find the concentration of
 using the equation:
using the equation:
![\[ [\text{H}_3O^+] = 10^{-\text{pH}} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/704juty1pog027u1c2m64ujza82pepdzd6.png)
Substitute the given pH value into the equation:
![\[ [\text{H}_3O^+] = 10^(-1.92) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/fepl28c2irk37grdv1je3e30887otbzqv4.png)
Calculate the concentration of
 . Now, since HF is a weak acid, we can assume that the concentration of
. Now, since HF is a weak acid, we can assume that the concentration of
 is the same as the concentration of
is the same as the concentration of
 (from the ionization equation). The concentration of HF is given as 0.23 M.
(from the ionization equation). The concentration of HF is given as 0.23 M.
Now, substitute the values into the expression for
 :
:
![\[ K_a = \frac{[\text{H}^+][\text{F}^-]}{[\text{HF}]} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/urdck4ygurvkmn4h8u9vtluzonmbrelykb.png)
![\[ K_a = ((10^(-1.92)) * (10^(-1.92)))/(0.23) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/yqt6ba4jzm3f2x5a4xiqg7ovfhavcgr1g0.png)
Calculate
 , and the result will match one of the given options. In this case, I'll calculate it:
, and the result will match one of the given options. In this case, I'll calculate it:
![\[ K_a = ((10^(-1.92)) * (10^(-1.92)))/(0.23) \approx 3.7 * 10^(-4) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/obrp5tw7fq2oc8gfih5mmyf7psv3gt7s71.png)
So, the correct answer is: