Question

Rhianna and Logan start at the same point and walk in the same direction. If Rhianna’s average velocity is (v_{{avg,R}}) and she walks for half of Logan’s time, what is Logan’s velocity (v_{{avg,L}}) if he walks three times as far?

a) (v_{{avg,L}} = 3v_{{avg,R}})
b) (v_{{avg,L}} = frac{3}{2}v_{{avg,R}})
c) (v_{{avg,L}} = frac{1}{2}v_{{avg,R}})
d) (v_{{avg,L}} = frac{1}{3}v_{{avg,R}})

Answer 1

Logan's average velocity is three times Rhianna's average velocity.

Step-by-step explanation:

To find Logan's average velocity in terms of Rhianna's average velocity, we need to consider the distances they walk and the time it takes for each of them. We are given that Rhianna walks for half of Logan's time and that Logan walks three times the distance. Average velocity is defined as the total displacement divided by the total time elapsed.

Since Rhianna and Logan walk in the same direction, we can say that Logan's displacement is three times Rhianna's displacement.

Using the equation for average velocity, we can set up the following ratio:

`(V_a_v_g, L) = (3V_a_v_g, R)`

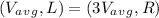
Therefore, Logan's average velocity is three times Rhianna's average velocity, which is represented by option a)
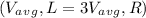`(V_a_v_g, L = 3V_a_v_g, R)`.