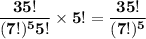Question

Exercise 10.10.2: Distributing a coin collection. About A man is distributing his coin collection with 35 coins to his five grandchildren. How many ways are there to distribute the coins if: (a) The coins are all the same. (b) The coins are all distinct. (c) The coins are the same and each grandchild gets the same number of coins (d) The coins are all distinct and each grandchild gets the same number of coins

Answer 1

Explanation:

Given that:

all coins are same;

The same implies that the number of the non-negative integral solution of the equation:

`x_1+x_2+x_3+x_4+x_5 = 35`

`x_1 > 0 ; \ \ \ x_1 \ \varepsilon \ Z`

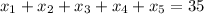
Thus, the number of the non-negative integral solution is:

`^((35+3-1))C_(5-1) = ^(39)C_4`

(b)

Here all coins are distinct.

So; the number of distribution appears to be an equal number of ways in arranging 35 different objects as well as 5 - 1 - 4 identical objects

i.e.

`= ((35+4)!)/(4!)`

`= (39!)/(4!)`

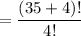
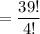
(c)

Here; provided that the coins are the same and each grandchild gets the same.

Then;

`x_1+x_2+x_3+x_4+x_5 = 35`

`x_1 > 0 ; \ \ \ x_1 \ \varepsilon \ Z`

`x_1=x_2=x_3=x_4=x_5`

`5x_1 = 35\\\\ x_1= (35)/(5) \\ \\ x_1= 7`

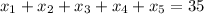
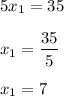
Thus, each child will get 7 coins

(d)

Here; we need to divide the 35 coins into 5 groups, this process will be followed by distributing the coin.

The number of ways to group them into 5 groups =
`(35!)/((7!)^55!)`

Now, distributing them, we have:

`\mathbf{(35!)/((7!)^55!) * 5!= (35!)/((7!)^5)}`