Question

How to turn into standard form

Answer 1

The hyperbola equation in standard form is:
`x^2` :
`(x + 1)^2/946` ,

`y^2` :
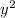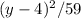`(y - 4)^2/59` ,Constant :1

Here's the step-by-step process of converting the equation to standard form:

Step 1: Complete the square for x.

Move the constant term to the right side of the equation:
`x^2 + 2x - 16y^2 + 64y - 79 = 0`

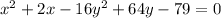
We want to complete
`x^2 + 2x` into a perfect square. To do that, we should add and subtract
`(1/2)^2 = 1`to it:
`x^2 + 2x + 1 - 1 - 16y^2 + 64y - 79 = 0`

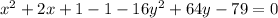
Rewrite the expression as
`(x + 1)^2 - 1 - 16y^2 + 64y - 79 = 0`

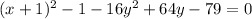
Step 2: Complete the square for y.

Move the constant terms to the right side of the equation:
`(x + 1)^2 - 1`-
`16y^2 + 64y - 79 = 0`

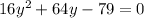
We want to complete
`-16y^2 + 64y` into a perfect square. To do that, we should add and subtract
`(-1/2 * 64)^2 = 1024` to it:

`(x + 1)^2 - 1 - 16y^2 + 64y + 1024 - 1024 - 79 = 0`

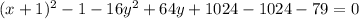
Rewrite the expression as
`(x + 1)^2 - 1 - 16(y - 4)^2 + 1024 - 79 = 0`

Step 3: Combine constant terms.

`(x + 1)^2 - 1 - 16(y - 4)^2 + 1024 - 79 = 0`

Combine the constant terms:
`(x + 1)^2 - 1 - 16(y - 4)^2 + 945 = 0`

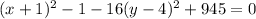
Step 4: Write the equation in standard form.

`(x + 1)^2/946 - (y - 4)^2/59` = 1

Therefore, the hyperbola equation in standard form is:

`x^2` :
`(x + 1)^2/946`

`y^2` :
`(y - 4)^2/59`

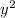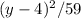
Constant :1