Answer:
P-value = 0.0046
Explanation:
Given that:
Sample size n = 290
sample mean
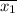 = 4.1
= 4.1
standard deviation
 = 0.6
= 0.6
population mean
 = 4.2
= 4.2
The null and the alternative hypothesis
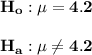
This is a two-tailed test.
The test statistics can be computed as:
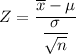
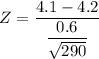
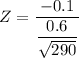
Z = -2.838
P-value = P(Z> 2.838)
P-value = P(Z< -2.838) +P(Z > 2.838)
P-value = 0.00227 + (1 - 0.9977)
P-value = 0.00457
P-value = 0.0046 (to 4 decimal places)