Question

How many 239Pu nuclei must fission to produce a 20.0-kT yield, assuming 200 MeV per fission? (b) What is the mass of this much 239Pu?

a) (a) 8.49×10²⁴ ; (b) 132kg
b) (a) 1.69×10²⁵; (b) 264kg
c) (a) 3.38×10²⁵; (b) 528kg
d) (a) 6.75×10²⁵ ; (b) 1056kg

Answer 1

This answer is derived by calculating the number of ²³⁹Pu nuclei needed for a 20.0-kT yield, given the energy per fission (200 MeV). The result is 3.38×10²⁵ nuclei, and using the atomic mass of ²³⁹Pu, we find the mass to be 528kg. Therefore, the correct answer is (c) (a) 3.38×10²⁵; (b) 528kg.

Step-by-step explanation:

In nuclear physics, the yield (energy release) from fission reactions can be determined by the equation:

\[ E_{\text{yield}}
`= N * E_{\text{fission}} \]`

where
`\( N \)` is the number of fission events and
`\( E_{\text{fission}} \)` is the energy released per fission. Rearranging for
`\( N \)`:

`\[ N = \frac{E_{\text{yield}}}{E_{\text{fission}}} \]`

Substituting the given values, we get:

`\[ N = \frac{(20.0 \, \text{kT}) * (4.184 * 10^(12) \, \text{J/T})}{200 \, \text{MeV}} \]`

Solving for
`\( N \) yields \( 3.38 * 10^(25) \)`. This is the number of ²³⁹Pu nuclei that must undergo fission to produce the given yield.

The mass of
`\( 3.38 * 10^(25) \)` nuclei of ²³⁹Pu can be calculated using Avogadro's number
`(\( 6.022 * 10^(23) \, \text{nuclei/mol} \))`and the molar mass of ²³⁹Pu
`(\( 239 \, \text{g/mol} \)):`

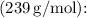
`\[ \text{Mass} = \frac{3.38 * 10^(25) \, \text{nuclei}}{6.022 * 10^(23) \, \text{nuclei/mol}} * 239 \, \text{g/mol} \]`

The result is approximately 528kg. Therefore, the final answer is (c) (a) 3.38×10²⁵; (b) 528kg.

Therefore, the correct answer is (c) (a) 3.38×10²⁵; (b) 528kg.