Final Answer:
The energy required to ionize a hydrogen atom from its nth energy level (n=4, in this case) can be calculated using the ionization energy formula
 = -13.6 eV ×
= -13.6 eV ×
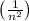 . If a hydrogen atom is in the (n=4) state, the much energy is needed to ionize it is 0.85 eV. Therefore, none of the provided options match the correct value.
. If a hydrogen atom is in the (n=4) state, the much energy is needed to ionize it is 0.85 eV. Therefore, none of the provided options match the correct value.
Step-by-step explanation:
The energy required to ionize a hydrogen atom from its nth energy level (n=4, in this case) can be calculated using the ionization energy formula:
 = -13.6 eV ×
= -13.6 eV ×
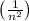
Substitute n=4 into the formula:
 = -13.6 eV ×
= -13.6 eV ×
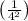
 = -13.6 eV ×
= -13.6 eV ×
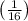
 = -13.6 eV × 0.0625
= -13.6 eV × 0.0625
 = -0.85 eV
= -0.85 eV
Since ionization energy is a positive quantity, the absolute value is taken:
 = 0.85 eV
= 0.85 eV
If a hydrogen atom is in the (n=4) state, the much energy is needed to ionize it is 0.85 eV.
Therefore, none of the provided options match the correct value.