Question

SOLUTION: a diver jumps from a diving board that is 24 feet above the water. the height of the diver is given by h= -16(t-1.5)(t+1) where the height h is measured in feet and the time t

Answer 1

The diver will hit the water at 1.5 seconds

Explanation:

Given

`h= -16(t-1.5)(t+1)`

Required (Missing from the question)

When will the diver hit the water?

To do this, we simply solve for t

When the diver hits the water, the height is 0 (at that point)

So, substitute 0 for h in
`h= -16(t-1.5)(t+1)`

`0= -16(t-1.5)(t+1)`

Divide both sides by -16

`(0)/(-16) =(-16(t-1.5)(t+1))/(-16)`

`(0)/(-16) =(t-1.5)(t+1)`

`0 =(t-1.5)(t+1)`

`(t-1.5)(t+1)=0`

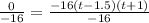
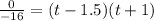
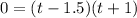
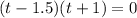
Split

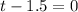`t - 1.5 = 0` or
`t + 1 = 0`

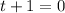
Solve for t

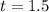`t = 1.5` or
`t = -1`

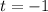
But time (t) can not be negative.

So:

`t = 1.5`

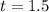
Hence, the diver will hit the water at 1.5 seconds