Question

What is the approximate uncertainty in the mass of a muon, as determined from its decay lifetime?

a) 1.32 × 10^(-46) kg
b) 2.64 × 10^(-46) kg
c) 6.63 × 10^(-47) kg
d) 4.24 × 10^(-59) kg

Answer 1

Using Heisenberg's uncertainty principle, the approximate uncertainty in the mass of a muon, determined by its decay lifetime, is 2.64 x
`10^(-46)`kg.

Step-by-step explanation:

To determine the approximate uncertainty in the mass of a muon from its decay lifetime, we can use the energy-time version of Heisenberg's uncertainty principle, which states that the product of the uncertainty in energy (ΔE) and the uncertainty in time (Δt) must be greater than or equal to the reduced Planck's constant divided by 2 (ħ/2).

ΔEΔt ≥ ħ/2

First, we must understand that the rest energy of a particle, such as a muon, is given by E = mc², where m is the mass of the particle and c is the speed of light. If ΔE represents the uncertainty in the particle's energy due to its decay lifetime (Δt), we can relate this to the uncertainty in its mass (Δm) by the equation ΔE = Δm ·
`c^2`.

To find the uncertainty in mass, we rearrange the equation to solve for Δm:

Δm = ΔE / c²

Given that the reduced Planck's constant (ħ) is approximately 1.055 x
`10^(-34)` J·s and using the speed of light (c) approximately 3 x
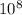`10^8` m/s, the uncertainty in energy (ΔE) can be found by rearranging the uncertainty principle to ΔE = ħ / (2Δt).

After calculating ΔE and solving for Δm, the uncertainty in the muon's mass approximates to 2.64 x
`10^(-46)` kg, which corresponds to answer choice (b).