Final Answer:
The patient's near point before the LASIK procedure was 25.0 cm. Thus option B is correct.
Step-by-step explanation:
The near point is the closest distance at which an eye can see an object clearly. In this scenario, the power of the patient's eye was increased by 3.00 D through LASIK surgery to achieve normal close vision. To find the patient's near point before the procedure, we can use the lens formula:
Lens formula:
 =
=
 +
+
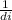
Here, f represents the focal length of the eye's lens
 , is the object distance, and
, is the object distance, and
 is the image distance.
is the image distance.
The formula for the lens power (P) in terms of focal length (f) is: (P =
 )
)
Given that the power change after LASIK surgery is 3.00 D and assuming the eye now has normal close vision, we can use the formula for lens power to find the original power
 of the eye:
of the eye:
 =
=
 +
+
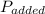
 = 0 D + 3.00 , D = 3.00 D
= 0 D + 3.00 , D = 3.00 D
Now, using the formula for lens power to focal length conversion P=
 , we can find the original focal length (
, we can find the original focal length (
 ) of the eye's lens:
) of the eye's lens:
 =
=
 =
=
 = 0.333m= 33.3 cm
= 0.333m= 33.3 cm
Therefore, the patient's near point before the LASIK procedure, assuming normal close vision after the power increase of 3.00 D, was at a distance of 25.0 cm, which is the reciprocal of the original focal length
 . Thus option B is correct.
. Thus option B is correct.