Question

. [30%] We first showed that The electric field for a point charge radiating in 3-dimensions has a distance dependence of 1/r 2 (see Equation 1). In Problem 1 you showed that the electric field for a point charge radiating in 2-dimensions has a distance dependence of 1/r . Consider again the 2-dimensional case described in Problem 1. What distance dependence do you expect for the electric potential

Answer 1

Answer is explained in the explanation section below.

Step-by-step explanation:

Note: This question is incomplete and lacks necessary data to solve. As it mentioned the reference of problem number 1, which is missing in this question. However, I have found that question on the internet and will be solving the question accordingly.

Solution:

The relation between electric field and the electric potential is:

E =
`(dV)/(dr)`

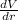
So, making dV the subject, we have:

dV = E x dr

Integrating the above equation, we get.

V =
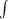`\int\limits^_ {} \,`E x dr Equation 1

Now, in 2-D

E is inversely proportional to the radius r.

E ∝ 1/r

So, we can write: replacing E ∝ 1/r in the equation 1

V ∝
`\int\limits^_ {} \,`
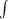
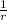`(1)/(r)` x dr

Which implies that,

V ∝ log (r)

Hence, distance dependence expected for the electric potential = ln (r)