Question

On your paper, construct a rectangle on a coordinate plane that satisfies these criteria.

• The sides of the rectangle are either vertical or horizontal.

• The perimeter of the rectangle is 42 units.

• Each of the vertices lies in a different quadrant.

What are the coordinates of the vertices of your rectangle? Explain how you know the perimeter of your rectangle is

42 units

Answer 1

`A = (5,3)`

`B = (-5,3)`

`C = (-5,-8)`

`D = (5,-8)`

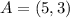
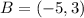
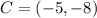
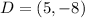
Explanation:

Required

`Perimeter = 42`

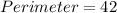
Construct a rectangle whose perimeter is 42 units and satisfies the given conditions.

First, name the rectangle ABCD.

Such that:

`A = (x_1,y_1)`

`B = (x_2,y_2)`

`C = (x_3,y_3)`

`D = (x_4,y_4)`

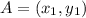
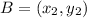
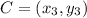
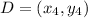
For the rectangle to be either horizontal or vertical, then:

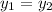`y_1 = y_2` and
`y_3 = y_4`

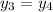
We have that:

`Perimeter = 42`

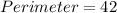
Replace perimeter with its formula

`2(AB + BC) = 42`

Divide both sides by 2

`AB + BC = 21`

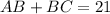
This implies that, the distance between adjacent sides (through the edges) must be equal to 21

Having said that: a set of coordinates that satisfy the given conditions are:

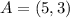`A = (5,3)` -- First quadrant

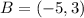`B = (-5,3)` -- Second quadrant

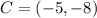`C = (-5,-8)` -- Third quadrant

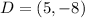`D = (5,-8)` -- Fourth quadrant

The above quadrants satisfy the condition:

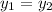`y_1 = y_2` and
`y_3 = y_4`

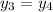
HOW TO KNOW THE PERIMETER IS 42

To do this, we simply calculate the distance between the edges and add them up

Distance is calculated as:

`D = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2`

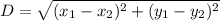
For AB

`A = (5,3)`

`B = (-5,3)`

`D_1 = √((5 - (-5))^2 + (3 - 3)^2)= √((10)^2 + (0)^2) = √(100) = 10`

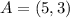
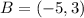
For BC

`B = (-5,3)`

`C = (-5,-8)`

`D_2 = √((-5 - (-5))^2 + (3 - (-8))^2)= √((0)^2 + (11)^2) = √(121) = 11`

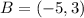
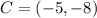
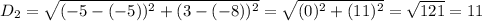
For CD

`C = (-5,-8)`

`D = (5,-8)`

`D_3 = √((-5 -5)^2 + (-8 - (-8))^2)= √((-10)^2 + (0)^2) = √(100) = 10`

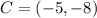
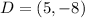
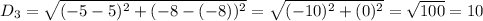
For DA

`D = (5,-8)`

`A = (5,3)`

`D_4 = √((5 -5)^2 + (-8 -3)^2)= √((0)^2 + (11)^2) = √(121) = 11`

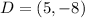
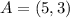
So, the perimeter is:

`P = D_1 + D_2 + D_3 + D_4`

`P = 10 + 11 + 10 +11`

`P = 42`

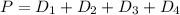
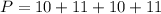
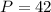
See attachment for rectangle