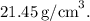Question

Platinum (atomic radius = 1.38 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of platinum.

Answer 1

The edge length of the face-centered cubic unit cell for platinum is 3.92 Å. The density of platinum is approximately
`\(21.45 \, \text{g/cm}^3\).`

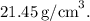
Step-by-step explanation:

*Calculating the Edge Length of a Face-Centered Cubic Unit Cell for Platinum*

In a face-centered cubic (FCC) structure, the relationship between the atomic radius (r) and the edge length (a) of the unit cell is given by the equation
`\(a = 2√(2) r\).`

For platinum, with an atomic radius of 1.38 Å, the edge length (a) of the FCC unit cell is calculated as follows:

`\[ a = 2√(2) * 1.38 = 3.92 \, \text{Å} \]`

*Calculating the Density of Platinum*

To calculate the density of platinum
`(\(\rho\))`, the formula is used:

`\[ \rho = \frac{\text{mass of atoms in a unit cell}}{\text{volume of the unit cell}} \]`

For an FCC structure, there are 4 atoms per unit cell. The mass of a platinum atom (atomic weight = 195.08 u) is converted to grams using Avogadro's number
`(\(6.022 * 10^(23) \, \text{atoms/mol}\))`.

The volume of the unit cell is
`\(a^3\)`. which, in this case, is
`\((3.92 \, \text{Å})^3\)`. Combining these values, we calculate the density of platinum as approximately
`\(21.45 \, \text{g/cm}^3\).`