Question

A vertical beam of power intensity P (in Watts/m2 ) passes downward through a particular substance. The rate at which P decreases with respect to the thickness t (in meters) through which the beam has passed is proportional to P(t). The power intensity P at the top of the substance is 3,000 W/m2 . The power intensity P at a depth of 2.00 meters below the surface is 600 W/m2 . What is the power intensity P at a depth of 1.25 meters below the surface

Answer 1

x = 1162.5 W/m²

Step-by-step explanation:

Since, the power decrease is proportional to the depth of the beam. Therefore, interpolation can be used to find the intensity of power at a depth of 1.25 m. First we calculate the slope from know points:

`Slope = (\Delta y)/(\Delta x) \\\\Slope = ((1500 - 3000)\ W/m^(2))/((2 - 0)\ m) \\\\Slope = -750\ W/m`

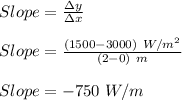
Now, we can find the unknown value by using this slope:

`Slope = -750\ W/m = ((600 - x)\ W/m^(2))/((2 - 1.25)\ m)\\\\(-750\ W/m)(0.75\ m) = (600 - x)\ W/m^(2)\\x = 600\ W/m^(2) + 562.5\ W/m^(2)\\`

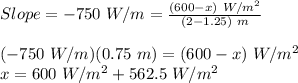
x = 1162.5 W/m² (Power intensity at depth of 1.25 m)