Answer:
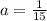
Explanation:
![\frac{\sqrt[5]{x} }{(x^(1)/(5) )^(4) } = x^(a)](https://img.qammunity.org/2024/formulas/mathematics/high-school/7jaeewirks5rffu3bwvfon69lgoaqb1bdx.png)
![\frac{\sqrt[5]{x} }{x^(4)/(5) } =x^a](https://img.qammunity.org/2024/formulas/mathematics/high-school/z9lgtmi36i4r3onk1wwvaw3o06btsi2tp0.png)
Fractional exponets according to the exponents properties the denominator can be changed to be a radical like this
![\frac{\sqrt[5]{x} }{\sqrt[5]{x^4} }](https://img.qammunity.org/2024/formulas/mathematics/high-school/5g0dbg5z11759r7cuny1pmx8v730ygeupq.png)
Now we can turn this into one big radical
![\sqrt[5]{(x)/(x^4) }](https://img.qammunity.org/2024/formulas/mathematics/high-school/rw8ansxjwf3u1gss4oojp4kjciuswhpmuz.png)
simplify
![\sqrt[5]{x^(1)/(3) }](https://img.qammunity.org/2024/formulas/mathematics/high-school/t8p6ur224xz3qn9umy25p19odmuu7xh8a4.png)
Now you can turn the radical into an exponent
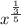
Simplify
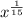
I really hope this helps I tried to find photos to show the rules I used but for some reason they won't save to my computer. Let me know if you have questions and if the answer was right