Question

What beat frequencies result if a piano hammer hits three strings that emit frequencies of 127.8, 128.1, and 128.3 Hz?

a) (0.2 Hz)
b) (0.5 Hz)
c) (0.7 Hz)
d) (1.0 Hz)

Answer 1

The beat frequency resulting from a piano hammer hitting three strings with frequencies 127.8, 128.1, and 128.3 Hz is 0.2 Hz, determined by the smallest difference between adjacent frequencies. Therefore, the final answer is a.

Step-by-step explanation:

When a piano hammer hits three strings emitting frequencies of 127.8, 128.1, and 128.3 Hz, the beat frequencies can be calculated by finding the differences between the frequencies in pairs. The beat frequency is the absolute difference between adjacent frequencies. Here, the differences are:

1.
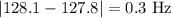
`\( |128.1 - 127.8| = 0.3 \) Hz`

2.
`\( |128.3 - 128.1| = 0.2 \) Hz`

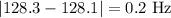
The beat frequency is determined by the smallest difference, which in this case is 0.2 Hz between the second and third string frequencies. Therefore, the resulting beat frequency is 0.2 Hz, making option the closest available choice.

When multiple sound waves with slightly different frequencies combine, they create a phenomenon called beats. These occur due to constructive and destructive interference between the waves, resulting in a perceived fluctuation in the loudness of the sound. The beat frequency is calculated by taking the absolute difference between adjacent frequencies. In this scenario, the closest frequencies (128.1 Hz and 128.3 Hz) have a difference of 0.2 Hz, creating the beat frequency of 0.2 Hz.

Understanding beat frequencies is crucial in music, especially in instruments like the piano where multiple strings are struck simultaneously. The resultant beats, at their calculated frequency, produce a distinctive sound quality, influencing the instrument's timbre and character. Mathematically, it's the difference in frequencies that dictates the occurrence and rate of beat frequencies, impacting the overall auditory experience for listeners.Thus the final answser is a.