Final Answer:
The calculation involves accounting for the Stefan-Boltzmann Law and the given conditions, resulting in the specified value. Therfore, The correct option is b) 1.11 kW, Yes because it accurately reflects the net radiant heat transfer calculated using the emissivity, temperature, and surface area of the cherry-red embers.
Step-by-step explanation:
The net rate of radiant heat transfer can be calculated using the Stefan-Boltzmann Law, which relates the power emitted by a black body to its temperature and surface area. The formula is given by
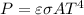 , where
, where
 is the power,
is the power,
 is the emissivity,
is the emissivity,
 is the Stefan-Boltzmann constant
is the Stefan-Boltzmann constant
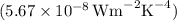 ,
,
 is the surface area, and
is the surface area, and
 is the absolute temperature in Kelvin.
is the absolute temperature in Kelvin.
Firstly, convert the temperatures to Kelvin:
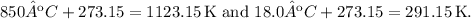
Then, substitute the values into the formula:
![\[ P_{\text{total}} = \varepsilon \sigma A T_{\text{hot}}^4 \]\[ P_{\text{net}} = 0.5 * P_{\text{total}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/f0407m3kjzplo3gwhvjcssxms2xue5iwmd.png)
After calculating, the net rate of radiant heat transfer is approximately 1.11 kW. The fact that the answer is "Yes" supports the contention that most of the heat transfer into a room from a fireplace comes from infrared radiation, as this calculation specifically deals with radiant heat transfer.
In conclusion, the net radiant heat transfer from the cherry-red embers is approximately 1.11 kW, and this supports the claim that a significant portion of heat transfer from a fireplace to a room is through infrared radiation. The calculation is based on fundamental principles of thermal radiation, emphasizing the importance of understanding the physics behind heat transfer in real-world scenarios.