Question

ou are given three pieces of wire that have different shapes (dimensions). You connect each piece of wire separately to a battery. The first piece has a length L and cross-sectional area A. The second is twice as long as the first, but has the same thickness. The third is the same length as the first, but has twice the cross-sectional area. Rank the wires in order of which carries the most current (has the lowest resistance) when connected to batteries with the same voltage difference. Rank the wires from most current (least resistance) to least current (most resistance). ResetHelp Least Current

Answer 1

i₃ > i₁ > i₂

Step-by-step explanation:

For this exercise we use the resistance ratio

R = ρ
`(l)/(A)`

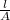
where ρ is the resistivity of the wire, in this case it is the same for all three cases, l the length and A the area of ​​the wire.

We have three cases

a) length l = L

area A = A

b) length l = 2L

area A = A

c) length l = L

area A = 2A

we calculate the resistance for each case

a) R₁ = ρ L / A

b) R₂ = ρ 2L / A

R₂ = 2 ρ L / A

R₂ = 2 R₁

c) R₃ = ρ L / 2A

R₃ = ½ ρ L / A

R₃ = 0.5 R₁

therefore when the connect of the circuit is carried out we can use ohm's law

V = i R

i = V / R

whereby

a) i₁ = V / R₁

b) i₂ = V / 2R₁

i₂ = ½ i₁

i₂ = 0.5 i₁

c) i₃ = V / 0.5 R₁

i₃ = 2 I₁

the order from highest to lowest in the current is

i₃ > i₁ > i₂