Question

Two identical point charges are fixed to diagonally opposite corners of a square that is 0.395 m on a side. Each charge is 4.0 x 10-6 C. How much work is done by the electric force as one of the charges moves to an empty corner

Answer 1

The work done by the electric force as one of the charges moves to an empty corner is:

`W=0.129\: J`

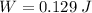
Step-by-step explanation:

The electric force between these points charges are:

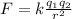`F=k(q_(1)q_(2))/(r^(2))` (1)

Where:

k is the coulomb constant (
`9*10^(9) Nm^(2)C^(-2)`)

q(1) the first charge

q(2) the second charge

r is the distance between them

The distance r is the distance of the diagonal of the square.

`r=\sqrt{0.395^(2)+0.395^(2)}`

`r=0.56\: m`

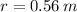
Then, using the equation (1) the electric force will be:

`F=9*10^(9)(16*10^(-12))/(0.56^(2))`

`\vec{F}=0.46\: N \vec{r}`

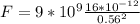
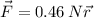
If we want to find the work done by the electric force we need to use the component of the force in the x or y direction because is the direction of the empty corner.

`F_(x)=Fcos(45)`

`W=F_(x)d`

`W=0.46cos(45)0.395`

`W=0.129\: J`

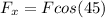
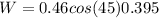
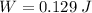
I hope it helps you!