Final Answer:
(a)
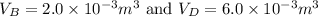
(b)
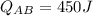
(c)

(d)
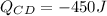
Step-by-step explanation:
a: The Carnot engine undergoes a cycle ABCDA, where AB is an isothermal expansion. Using the ideal gas law and the fact that AB is isothermal, we can find
 .
.
The volumes at A and C are given, and the temperatures at the two ends are known. Thus, the gas law \(PV = nRT\) helps calculate the volumes.
b: For the heat absorbed during the isothermal expansion AB, the formula
 is used, where \(C_v\) is the molar heat capacity at constant volume.
is used, where \(C_v\) is the molar heat capacity at constant volume.
The temperature change \(\Delta T\) during AB can be found from the temperatures of the two thermal baths.
c: The work done during AB, \(W_{AB}\), is given by the equation \(W = nRT\ln(V_B/V_A)\), where
 is the initial volume. The negative sign indicates work done on the gas.
is the initial volume. The negative sign indicates work done on the gas.
d: During the CD isothermal expansion, the gas releases heat
 which is equal in magnitude but opposite in sign to the heat absorbed in AB due to the second law of thermodynamics. The work done during CD is analogous to AB but with different initial and final volumes.
which is equal in magnitude but opposite in sign to the heat absorbed in AB due to the second law of thermodynamics. The work done during CD is analogous to AB but with different initial and final volumes.