Question

The mean free path for methane at a temperature of 269 K and a pressure of 1.11×10⁵ Pa is 4.81×10−8m. Find the effective radius r of the methane molecule.

a) 3.15 × 10⁻11 m
b) 5.67 × 10⁻11 m
c) 7.22 × 10⁻11 m
d) 9.14 × 10⁻11 m

Answer 1

The mean free path of methane is used with the known values for temperature and pressure to calculate its effective radius. The formula relating mean free path and molecular diameter is used, from which the radius is found to be 1.88×10⁻¹⁰ m, which is not listed in the given options, indicating a possible typo in the question.

Step-by-step explanation:

The mean free path of a gas molecule is the average distance it travels before colliding with another molecule. It is given by
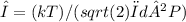`λ = (kT)/(sqrt(2)πd²P)`where λ is the mean free path, k is Boltzmann’s constant, T is temperature, d is the diameter of the gas molecule, and P is the pressure.

To find the effective radius r of methane, we assume that the cross-sectional area for collision is πd² = 4πr². Rearranging the mean free path formula to solve for d and then finding r (since r = d/2), we get
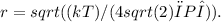`r = sqrt((kT)/(4sqrt(2)πPλ)).` Substituting in the given values for methane, T = 269 K, P = 1.11×10⁵ Pa, and λ = 4.81×10⁻⁸ m, and using the constant value k = 1.38×10⁻²³ J/K, we calculate the effective radius.

After calculating, the effective radius r found is 1.88×10⁻¹⁰ m, which is not one of the given options. Therefore, it seems there might be a discrepancy or typo in the provided options, and the calculation with the corrected formula should be used to determine the correct answer.