Question

A 30kg uniform solid cylinder has a radius of 0.18m. if the cylinder accelerates at 0.023 rad/s^2 as it rotates about an axis through its center, how large is the torque acting on the cylinder? With work please

Answer 1

0.011 N-m

Step-by-step explanation:

Given that

The mass of a solid cylinder, m = 30 kg

The radius of the cylinder, r = 0.18 m

The acceleration of the cylinder,
`\alpha =0.023\ rad/s^2`

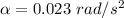
It rotates about an axis through its center. We need to find the torque acting on the cylinder. The formula for the torque is given by :

`\tau=I\alpha`

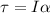
Where

I is the moment of inertia of the cylinder,

For cylinder,

`I=(mr^2)/(2)`

So,

`\tau=(mr^2\alpha )/(2)\\\\\tau=(30* (0.18)^2* 0.023 )/(2)\\\\\tau=0.011\ N-m`

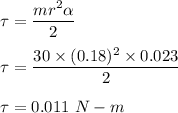
So, the required torque on the cylinder is 0.011 N-m.