Final Answer:
To ensure a constant difference in length of (0.500 m) regardless of temperature, the engineer should design the steel beam to be approximately twice as long as the aluminum beam.
Step-by-step explanation:
To maintain a constant difference in length between the steel and aluminum beams, regardless of temperature changes, we can use the formula for linear expansion:
![\[ \Delta L = L_0 \alpha \Delta T \]](https://img.qammunity.org/2024/formulas/physics/high-school/ouq9jauupp10td69gtrj23e34z2qo9dxzg.png)
where
 is the change in length,
is the change in length,
 is the original length,
is the original length,
 is the coefficient of linear expansion, and
is the coefficient of linear expansion, and
 is the change in temperature.
is the change in temperature.
Since the problem specifies a constant difference in length
 we can set up a ratio of the lengths of the steel
we can set up a ratio of the lengths of the steel
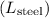 and aluminum
and aluminum
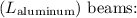
![\[ \frac{L_{\text{steel}}}{L_{\text{aluminum}}} = 2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/cc148k9jd52fi6dg1kwr498pk9uigngs1q.png)
This ensures that the steel beam is approximately twice as long as the aluminum beam, maintaining a consistent difference in length of
 for ordinary temperature changes.
for ordinary temperature changes.
b) Designing for temperature changes is crucial in preventing structural issues. Temperature variations can lead to expansions or contractions in materials, affecting the stability and integrity of structures. The engineer must consider the coefficient of linear expansion
 for each material, ensuring that the designed structure can accommodate temperature fluctuations without compromising its functionality or safety.
for each material, ensuring that the designed structure can accommodate temperature fluctuations without compromising its functionality or safety.
c) The coefficient of linear expansion is not irrelevant to the solution. It is a fundamental parameter that defines how a material's dimensions change with temperature. In this case, the choice of materials (steel and aluminum) and their respective coefficients of linear expansion play a pivotal role in achieving the desired design outcome. The engineer needs to consider these coefficients to ensure the structure's stability under varying temperature conditions.