Question

(a) Sketch a graph of the potential energy function U(x)=kx2/2+Ae−αx2, where k,A,andα are constants.

(b) What is the force corresponding to this potential energy?
(c) Suppose a particle of mass m moving with this potential energy has a velocity va when its position is x=a. Show that the particle does not pass through the origin unless; A≤mva2+ka22(1−e−αa2).

Answer 1

(a) The potential energy function graph is a parabola with an additional Gaussian term, forming a well-like structure.

(b) The force corresponding to this potential energy is given by
`F(x) = -dU/dx = -kx - 2Aαxe^(-αx²).`

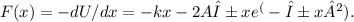
(c) The particle does not pass through the origin unless
`A ≤ mva² + (ka²/2)(1 - e^(-αa²)).`

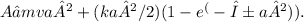
Step-by-step explanation:

(a) The potential energy function U(x) combines a harmonic term (kx²/2) and a Gaussian term (Ae^(-αx²)). The harmonic term contributes to a parabolic shape, typical for spring-like potentials, while the Gaussian term introduces a decaying exponential behavior, creating a well-like structure.

(b) The force corresponding to the potential energy is the negative derivative of the potential energy with respect to position, F(x) = -dU/dx. For the given U(x), the force function is
`F(x) = -kx - 2Aαxe^(-αx²).` The first term represents the force from the harmonic potential, while the second term arises from the Gaussian potential.

(c) Considering a particle of mass m with velocity va at position x=a, we evaluate the condition for the particle not to pass through the origin. This condition is given by
`A ≤ mva² + (ka²/2)(1 - e^(-αa²)),` indicating that the amplitude of the Gaussian term must be limited to ensure that the particle does not cross the origin. This result stems from the interplay between the kinetic and potential energy terms in the context of the given potential energy function.