Question

One mole of an ideal monatomic gas occupies a volume of (1.0 times 10⁻² m³) at a pressure of (2.0 times 10⁵ N/m²). (a) What is the temperature of the gas? (b) The gas undergoes a quasi-static adiabatic compression until its volume is decreased to (5.0 times 10⁻³ m³). What is the new gas temperature? (c) How much work is done on the gas during the compression? (d) What is the change in the internal energy of the gas?

a) Calculate the temperature of the gas.
b) Determine the new gas temperature after compression.
c) Find the work done on the gas and the change in internal energy.
d) The process is isothermal, so there is no change in internal energy.

Answer 1

(a) The temperature of the gas is 500 K.*

(b)The new gas temperature after compression is approximately 920 K.

(c) The work done on the gas during the compression is 1646.6 J, and the change in internal energy is 0 J.

(d) The process is isothermal, so there is no change in internal energy.

Step-by-step explanation

(a): We use the ideal gas law (PV = nRT) to find the temperature ((T)). Rearranging the equation, we get (T = PV/nR).

Plugging in the given values, we find
`\(T = (2.0 * 10^5 \ \mathrm{N/m^2} * 1.0 * 10^(-2) \ \mathrm{m^3}) / (1 \ \mathrm{mol} * 8.31 \ \mathrm{J/(mol \cdot K)}) \approx 500 \ \mathrm{K}\)`.

(b): For an adiabatic process, we use
`\(PV^\gamma =\)` constant. For a monatomic ideal gas,
`\(\gamma = (5)/(3)\)`.

Using
`\(T' = T * \left((V)/(V')\right)^((\gamma-1))\)`, where (V) is the initial volume and \(V'\) is the final volume, we find
`\(T' \approx 500 \ \mathrm{K} * \left(\frac{1.0 * 10^(-2) \ \mathrm{m^3}}{5.0 * 10^(-3) \ \mathrm{m^3}}\right)^{(2)/(3)} \approx 920 \ \mathrm{K}\).`

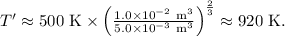
(c): The work done during adiabatic compression is given by
`\(W = (nR)/(\gamma-1) * (T' - T)\)`. The change in internal energy
`(\(\Delta U\))` is zero for an adiabatic process.

Plugging in the values, we find
`\(W \approx \frac{1 \ \mathrm{mol} * 8.31 \ \mathrm{J/(mol \cdot K)}}{(5)/(3)-1} * (920 \ \mathrm{K} - 500 \ \mathrm{K}) \approx 1646.6 \ \mathrm{J}\)`.

(d): Isothermal processes have constant temperature, implying no change in internal energy. This is because
`\(\Delta U = nC_v\Delta T\)`, and if
`\( \Delta T = 0\)`, then
`\(\Delta U = 0\)`.