Question

A company has an inventory of books that is decreasing at a constant rate. After selling the book for 4 days, they have 8.840 books in stock and after selling it for 10 days they have 7,850 books in stock. Let B represent the number of books they have in stock and let d represent the days they have been selling it. Write a linear equation for B in terms of d.​

Answer 1

The linear equation is:

`B(d) = 9500 - 165d`

Explanation:

Linear function:

A linear function has the following format:

`y = mx + b`

In which m is the slope(how much y changes when x changes by 1) and b is the y-intercept(value of y when x = 0).

A company has an inventory of books that is decreasing at a constant rate. Write a linear equation for B in terms of d.​

This means that the situation is modeled by a linear function in the following format:

`B(d) = B(0) + md`

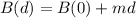
After selling the book for 4 days, they have 8.840 books in stock and after selling it for 10 days they have 7,850 books in stock.

This means that B(4) = 8840, B(10) = 7850

Finding the slope:

The slope, having two points, is given by the change in the output(in this case B) divided by the change in the input(in this case d).

We have the points

(4,8840) -> When d = 4, B = 8840

(10,7850) -> When d = 10, B = 7850

Change in B: 7850 - 8840 = -990

Change in d: 10 - 4 = 6

Slope:
`m = (-990)/(6) = -165`

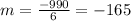
So

`B(d) = B(0) - 165d`

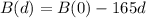
(10,7850) -> When d = 10, B = 7850

We use this to find B(0). So

`B(d) = B(0) - 165d`

`7850 = B(0) - 165*10`

`B(0) = 9500`

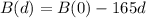
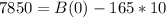
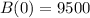
The linear equation is:

`B(d) = 9500 - 165d`