Question

Two slits 4.0×10−6m apart are illuminated by light of wavelength 600 nm. What is the highest order fringe in the interference pattern?

a. 1667
b. 2500
c. 5000
d. 3333

Answer 1

The highest order fringe in the interference pattern is given by option (d) 3333. In a double-slit interference pattern, the highest order fringe can be determined using the formula
`\(m_{\text{max}} = (d)/(\lambda)\),` where
`\(m_{\text{max}}\)` is the highest order fringe,
`\(d\)` is the slit separation, and
`\(\lambda\)` is the wavelength of light. Substituting the given values, we get
`\(m_{\text{max}} = (4.0 * 10^(-6))/(600 * 10^(-9)) = 3333\)`. Hence, the correct answer is (d) 3333.

Step-by-step explanation:

In a double-slit interference pattern, the condition for constructive interference is given by the path difference between the two slits being a whole number of wavelengths. The formula for calculating the highest order fringe is
`\(m_{\text{max}} = (d)/(\lambda)\`), where
`\(m_{\text{max}}\)` is the highest order fringe,
`\(d\)` is the slit separation
`(4.0×10^(-6) m), and \(\lambda\)` is the wavelength of light
`(600 nm or 600 * 10^(^-^9^) m).`

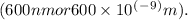
Substituting the values into the formula, we get
`\(m_{\text{max}} = (4.0 * 10^(-6))/(600 * 10^(-9))\)`. Simplifying this expression yields
`\(m_{\text{max}} = 3333\)`. Therefore, the highest order fringe in the interference pattern is 3333.

In summary, option (d) 3333 is the correct answer because it represents the highest order fringe, which is determined by the slit separation and the wavelength of light in the double-slit interference pattern.

Hence, the correct answer is (d) 3333.