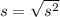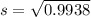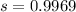Answer:
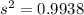 --- sample variance
--- sample variance
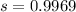 --- sample standard deviation
--- sample standard deviation
Explanation:
Given

Required
Calculate the sample variance and sample standard deviation
First, we calculate the midpoint of each class:

The midpoints are calculated by taking the average of the class intervals.
For instance:
Class 116.1 to 120.0 has a midpoint of
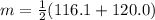


The same approach is applied to other classes.
Next, is to calculate the mean:
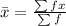
In this case, it is:
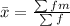
Where
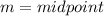
So, we have:
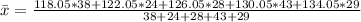
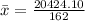

The sample variance (s^2) is:
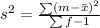
This gives:
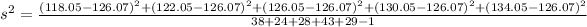
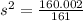
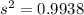
The sample standard deviation (s) is: