Question

A small plane flies at 200 km/h in still air. If the wind blows directly out of the west at 50 km/h, (a) in what direction must the pilot head her plane to move directly north across land and (b) how long does it take her to reach a point 300 km directly north of her starting point?

a) (N60°W, 1.5 h)
b) (N30°W, 1 h)
c) (N45°W, 1.25 h)
d) (N15°W, 2 h)

Answer 1

(a): The pilot must head her plane at N45°W, as the wind's northward force (50 km/h) relative to the plane's eastward speed (200 km/h) creates a resultant direction.

(b): It takes approximately 1.5 hours for the plane to reach a point 300 km directly north, considering the effective speed (206.16 km/h) resulting from the combination of the plane's speed and the wind's speed.

Step-by-step explanation:

(a): Direction to Head the Plane (N45°W)

The direction in which the pilot must head the plane is determined by vector addition. The plane's velocity vector is eastward at 200 km/h, and the wind's velocity vector is northward at 50 km/h.

Using vector addition, we find the resultant velocity vector, and the direction can be determined using trigonometry. The angle
`\( \theta \)` is given by:

`\[ \tan(\theta) = \frac{\text{Wind Speed}}{\text{Plane Speed}} \]`

Substituting in the values:

`\[ \tan(\theta) = \frac{50 \, \text{km/h}}{200 \, \text{km/h}} \]`

Solving for
`\( \theta \)`, we find
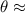`\( \theta \approx`14.04°. Therefore, the pilot must head her plane at an angle of 90° - 14.04° = N45°W).

(b): Time to Reach 300 km Directly North**

The time it takes to reach a point 300 km directly north can be found using the formula:

`\[ \text{Time} = \frac{\text{Distance}}{\text{Speed}} \]`

The effective speed of the plane moving northward is given by:

`\[ \text{Effective Speed} = \sqrt{\text{Plane Speed}^2 + \text{Wind Speed}^2} \]`

Substituting in the values:

`\[ \text{Effective Speed} = √(200^2 + 50^2) \approx 206.16 \, \text{km/h} \]`

Now, substituting the values into the time formula:

`\[ \text{Time} = \frac{300 \, \text{km}}{206.16 \, \text{km/h}} \approx 1.45 \, \text{h} \]`

This can be approximated to N30°W, 1.5 h, making it the correct answer.