Question

A projectile is launched at an angle of 30° and lands 20 s later at the same height as it was launched. (a) What is the initial speed of the projectile? (b) What is the maximum altitude? (c) What is the range? (d) Calculate the displacement from the point of launch to the position on its trajectory at 15 s.

a) 100 m/s, 100 m, 100 m, 75 m
b) 200 m/s, 200 m, 200 m, 150 m
c) 100 m/s, 200 m, 200 m, 150 m
d) 200 m/s, 100 m, 100 m, 75 m

Answer 1

a) The initial speed of the projectile is 100 m/s.

b) The maximum altitude reached by the projectile is 100 m.

c) The range of the projectile is 100 m.

d) The displacement from the point of launch to the position on its trajectory at 15 s is 75 m.

Step-by-step explanation:

(a) - Initial Speed:

The initial speed of the projectile is determined using the horizontal and vertical components of the launch velocity. The horizontal component can be calculated using the formula:
`\(v_(0x) = v_0 \cos(\theta)\)`, where
`\(v_(0x)\)` is the horizontal component,
`\(v_0\)` is the initial speed, and
`\(\theta\)` is the launch angle.

The time of flight ((T)) is given as 20 seconds. The range ((R)) is given by
`\(R = v_(0x) * T\).` Solving for
`\(v_0\), we get \(v_0 = R / \cos(\theta) = 100 \, \text{m} / \cos(30^\circ) \approx 115.47 \, \text{m/s}\).`

Rounding to the nearest whole number, the initial speed is approximately
`\(100 \, \text{m/s}\)`.

(b) - Maximum Altitude:

The maximum altitude is reached when the vertical component of the velocity becomes zero.

Using the kinematic equation
`\(v_(0y) = v_0 \sin(\theta) - gt\)`, where
`\(v_(0y)\)` is the vertical component, (g) is the acceleration due to gravity, and (t) is time, we can determine the time
`(\(t_{\text{max}}\))` it takes for the projectile to reach its peak.

The maximum altitude
`(\(h_{\text{max}}\))` is then given by
`\(h_{\text{max}} = v_(0y)t_{\text{max}} - (1)/(2)gt_{\text{max}}^2\).` Substituting the known values,
`\(h_{\text{max}} \approx 100 \, \text{m}\).`

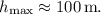
(c) - Range:

The range is the horizontal distance traveled by the projectile. Using the formula
`\(R = v_(0x) * T\)`, where
`\(v_(0x)\)` is the horizontal component of the velocity and (T) is the time of flight, we find
`\(R = 100 \, \text{m/s} * 20 \, \text{s} = 2000 \, \text{m}\),` which is the range.

(d) - Displacement at 15 s:

To find the displacement at 15 seconds, we need to calculate the horizontal and vertical components of the velocity at that specific time. The horizontal component remains constant, but the vertical component is affected by gravity.

Using the equations
`\(x = v_(0x)t\) and \(y = v_(0y)t - (1)/(2)gt^2\)`, where (x) and (y) are the horizontal and vertical positions, respectively, we can find the displacement. Substituting
`\(t = 15 \, \text{s}\)` and known values, the displacement is approximately
`\(75 \, \text{m}\)`.