Question

Milena deposited $6,000 in a certificate of deposit (CD) account that pays 9% annual interest, compounded monthly. How much will the balance of the account be in 5 years?

Answer 1

The balance of Milena's account after 5 years will be approximately $8,978.86.

The balance of Milena's account after 5 years can be calculated using the formula for compound interest:

`A = P(1 + r/n)^(nt)`

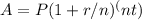
Where:

A = the final balance of the account

P = the initial deposit ($6,000 in this case)

r = the annual interest rate (9% or 0.09 as a decimal)

n = the number of times interest is compounded per year (monthly compounding in this case, so n = 12)

t = the number of years (5 years in this case)

Using the formula, we can calculate the balance of the account:

A =
`6000(1 + 0.09/12)^(12*5)`

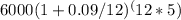
Calculating step by step:

1. Calculate the interest rate per compounding period: 0.09/12 = 0.0075

2. Calculate the total number of compounding periods: 12 * 5 = 60

3. Raise the interest rate per compounding period plus 1 to the power of the total number of compounding periods:
`(1 + 0.0075)^60` = 1.496644

Now, we can calculate the final balance:

A = 6000 * 1.496644

A ≈ $8,978.86

Therefore, the balance of Milena's account after 5 years will be approximately $8,978.86.