Question

. A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared. Is there evidence that the machine should be stopped and production wait for repairs

Answer 1

The calculated value |t| = |-3.082| =3.082 > 2.0322 at 0.05 level of significance

The null hypothesis is rejected

An alternative hypothesis is accepted

There is evidence that the machine should be stopped and production wait for repairs

Explanation:

Step(i):-

Given that the mean of the Population(μ) = 8 ounces

Given that the sample size 'n' = 35

The mean of the sample(x⁻) = 7.91

The variance of the sample S² = 0.03 ounces

S = √0.03 = 0.1732

Step(ii):-

Null Hypothesis: H₀: There is no evidence that the machine should be stopped and production wait for repairs

Alternative Hypothesis: H₁: There is evidence that the machine should be stopped and production wait for repairs

`t = (x^(-) -mean)/((S)/(√(n) ) )`

`t = (7.91 -8)/((0.1732)/(√(35) ) )`

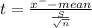
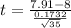
t = - 3.082

|t| = |-3.082| =3.082

Degrees of freedom

ν = n-1 = 35-1=34

t₀.₀₅ = 2.0322

The calculated value |t| = |-3.082| =3.082 > 2.0322 at 0.05 level of significance

The null hypothesis is rejected

An alternative hypothesis is accepted

conclusion:-

There is evidence that the machine should be stopped and production wait for repairs