Question

The graph shows that f(x)=(one-third) Superscript x is translated horizontally and vertically to get the function (one-third) Superscript x minus h.

Answer 1

The value of K is option B. -3.

How did we get the value?

The graph shows that
`f(x) = (1)/(3)^x` is translated horizontally and vertically to get the function
`g(x) = (1)/(3)^((x-h)) + k`

As the function g(x) goes down three units on the y-axis then the value of k is -3. So the correct option is option B. -3.

To solve for the value of h, we use the condition (4, 0).

we have;

`0 = (1/3) ^ (4 - h) - 3 * (1/3) ^ (4 - h) \\= 3 * ln(1/3) ^ (4 - h) \\= ln(3) * (4 - h) * ln(1/3) \\= ln(3) * 4 - h \\= (ln(3))/(ln(1/3)) * h \\= 4 - (ln(3))/(ln(1/3)) \\= 5`

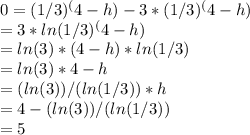
It could then be concluded that h is 5.

Complete question:

The graph shows that f(x)=(one-third) Superscript x is translated horizontally and vertically to get the function (one-third) Superscript (x minus h) plus k. What is the value of K?

a. -5

b. -3

c. 3

d. 5