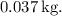Therefore, the mass of steam that must be condensed is approximately
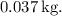
To solve this problem, we need to consider the heat transfer involved in two processes: first, raising the temperature of the glass and water, and second, condensing steam into water.
1. Heat transfer to raise the temperature of the glass and water:
![\[ Q_1 = m_{\text{glass}} \cdot c_{\text{glass}} \cdot \Delta T_{\text{glass}} + m_{\text{water}} \cdot c_{\text{water}} \cdot \Delta T_{\text{water}} \]](https://img.qammunity.org/2024/formulas/physics/college/7nnplcow1uzv1oxko29yhs4snqlqwffitm.png)
Where:


 is the change in temperature of the glass,
is the change in temperature of the glass,
 is the mass of water,
is the mass of water,
 is the specific heat capacity of water,
is the specific heat capacity of water,
 is the change in temperature of the water.
is the change in temperature of the water.
2. Heat transfer to condense steam into water:
![\[ Q_2 = m_{\text{steam}} \cdot L \]](https://img.qammunity.org/2024/formulas/physics/college/m608qu01xcbzigwbuc1il0s1tysnps89ys.png)
Where:
-
 is the mass of steam,
is the mass of steam,
-
 is the latent heat of vaporization.
is the latent heat of vaporization.
The total heat transfer
 is the sum of
is the sum of
 and
and
 :
:
![\[ Q_{\text{total}} = Q_1 + Q_2 \]](https://img.qammunity.org/2024/formulas/physics/college/pj1qc10sdst8lz91l7umme1uurx9ghu077.png)
Now, let's substitute the given values:
-
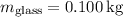
-
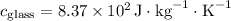
-
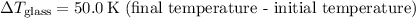
-

-
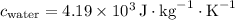
-
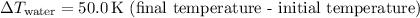
-
 is what we're trying to find.
is what we're trying to find.
-
 :
:
![\[ Q_1 = (0.100 \, \text{kg} \cdot 8.37 * 10^2 \, \text{J} \cdot \text{kg}^(-1) \cdot \text{K}^(-1) \cdot 50.0 \, \text{K}) + (0.200 \, \text{kg} \cdot 4.19 * 10^3 \, \text{J} \cdot \text{kg}^(-1) \cdot \text{K}^(-1) \cdot 50.0 \, \text{K}) \]](https://img.qammunity.org/2024/formulas/physics/college/578jbqvkghjd5lhxgpyi3y49bloxcof5rq.png)
![\[ Q_1 = 4.185 * 10^4 \, \text{J} + 4.185 * 10^4 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/college/1agra0h4et6b305rhm0kc2fhvm8lvptnx2.png)
![\[ Q_1 = 8.37 * 10^4 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/college/gqv53y4gtfo1mf0fdjpiueqjdkkgxfabwy.png)
Now, let's find
 :
:
![\[ Q_2 = m_{\text{steam}} \cdot L \]](https://img.qammunity.org/2024/formulas/physics/college/m608qu01xcbzigwbuc1il0s1tysnps89ys.png)
![\[ 8.37 * 10^4 \, \text{J} + m_{\text{steam}} \cdot 2.26 * 10^6 \, \text{J} \cdot \text{kg}^(-1) \]](https://img.qammunity.org/2024/formulas/physics/college/9saiiy12nwxfg4kj4xcy3pxjpjxylj7hdv.png)
Solving for
 :
:
![\[ m_{\text{steam}} = \frac{8.37 * 10^4 \, \text{J}}{2.26 * 10^6 \, \text{J} \cdot \text{kg}^(-1)} \]](https://img.qammunity.org/2024/formulas/physics/college/7p7aaqgt4864bza8pjirstkra7ngi1lcr2.png)
![\[ m_{\text{steam}} \approx 0.037 \, \text{kg} \]](https://img.qammunity.org/2024/formulas/physics/college/eyxnoe2j2esqhrteiigg4fnrxi61zeb7lh.png)
Therefore, the mass of steam that must be condensed is approximately