Question

The line x − y = 2 is on a coordinate plane and contains EF, which is one side of square EFGH. What is the slope of the line that contains FG?

(Please actually answer and not do some gibberish answer, I really need help with this.)

Answer 1

The slope of FG is -1

Explanation:

Given

Square EFGH

EF:
`x - y = 2`

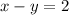
Required

Determine the slope of FG

First, we calculate the slope of EF

`x - y = 2`

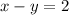
Make y the subject

`-y = 2 - x`

`y = x -2`

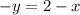
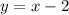
The general equation has the form:
`y = mx + b`

Where

`m = slope`

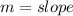
Compare
`y = mx + b` to
`y = x -2`

`m = 1`

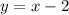
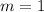
From the name of the square EFGH, we can conclude that EF and FG are perpendicular

The relationship between perpendicular lines is:

`m_2 = -(1)/(m_1)`

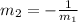
Where

`m_1 = m = 1` -- Slope of EF

and

m2 = slope of FG

Substitute 1 for m1 in
`m_2 = -(1)/(m_1)`

`m_2 = -(1)/(1)`

`m_2 = -1\\`

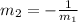
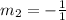
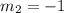
Hence, the slope of FG is -1