Question

A simple random sample of 85 students is taken from a large university on the West Coast to estimate the proportion of students whose parents bought a car for them when they left for college. When interviewed, 51 students in the sample responded that their parents bought them a car. What is a 95% confidence interval for p, the population proportion of students whose parents bought a car for them when they left for college

Answer 1

95% confidence interval for p, the population proportion of students whose parents bought a car for them when they left for college

(0.4958 , 0.7041)

Explanation:

Step(i):-

Given that the sample size 'n' = 85

The sample proportion

`p = (x)/(n) = (51)/(85) = 0.6`

95% confidence interval for p, the population proportion of students whose parents bought a car for them when they left for college

`(p^(-) -Z_(0.05) \sqrt{(p(1-p))/(n) } , p^(-) +Z_(0.05) \sqrt{(p(1-p))/(n) })`

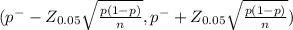
Step(ii):-

Given that the level of significance

α = 0.05

Z₀.₀₅ = 1.96

`(0.6 -1.96 \sqrt{(06(1-06))/(85) } , 0.6 +1.96 \sqrt{(0.6(1-0.6))/(85) })`

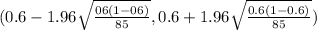
(0.6 - 0.104138 , 0.6 +0.104138)

(0.4958 , 0.7041)

Final answer:-

95% confidence interval for p, the population proportion of students whose parents bought a car for them when they left for college

(0.4958 , 0.7041)