Question

A car initially traveling at 27.2 m/s undergoes a constant negative acceleration of magnitude 1.90 m/s2 after its brakes are applied. (a) How many revolutions does each tire make before the car comes to a stop, assuming the car does not skid and the tires have radii of 0.325 m

Answer 1

Therefore, the revolutions that each tire makes is:

`\Delta \theta=22\: rev`

Step-by-step explanation:

We can use the following equation:

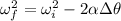`\omega_(f)^(2)=\omega_(i)^(2)-2\alpha \Delta \theta` (1)

The angular acceleration is:

`a_(tan)=\alpha R`

`\alpha=(1.9)/(0.325)`

`\alpha=5.85\: rad/s^(2)`

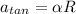
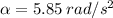
and the initial angular velocity is:

`\omega_(i)=(v)/(R)`

`\omega_(i)=(27.2)/(0.325)`

`\omega_(i)=83.69\: rad/s`

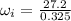
Now, using equation (1) we can find the revolutions of the tire.

`0=83.69^(2)-2*25.85 \Delta \theta`

`\Delta \theta=135.47\: rad`

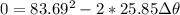
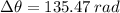
Therefore, the revolutions that each tire makes is:

`\Delta \theta=22\: rev`

I hope it helps you!