Question

AB is formed by A(-10, 3) and B(2.7). If line l is the perpendicular bisector of

AB

write the equation ofl in slope-intercept form.

Answer 1

Given:

AB is formed by A(-10, 3) and B(2,7). If line l is the perpendicular bisector of AB.

To find:

The equation of line l in slope intercept form.

Solution:

Slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

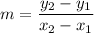
Slope of line AB is

`m_1=(7-3)/(2-(-10))`

`m_1=(4)/(2+10)`

`m_1=(4)/(12)`

`m_1=(1)/(3)`

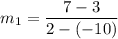
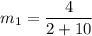
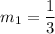
Product of slopes of two perpendicular lines is -1.

`m_1* m_2=-1`

`(1)/(3)* m_2=-1`

`m_2=-3`

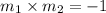
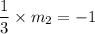
Midpoint of AB is

`Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`Midpoint=\left((-10+2)/(2),(3+7)/(2)\right)`

`Midpoint=\left((-8)/(2),(10)/(2)\right)`

`Midpoint=\left(-4,5\right)`

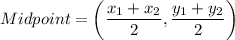
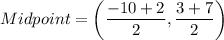
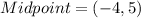
The perpendicular bisector of AB (i.e., line l)passes through he midpoint of AB, i.e., (-4,5) and having slope -3.

So, the equation of line l is

`y-y_1=m(x-x_1)`

`y-5=-3(x-(-4))`

`y-5=-3(x+4)`

`y=-3x-12+5`

`y=-3x-7`

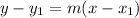
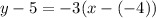
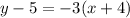
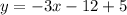
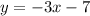
Therefore, the equation of line l in slope intercept form is
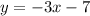`y=-3x-7`.