Question

Can someone plz help me with this and explain how to do this math problem

Answer 1

greater

Explanation:

the reason is because if you allow x to have a value that is less than 3,

`√(x - 3)`

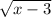
will produce a square root of a negative number, and the square root of a negative number requires the use of imaginary numbers, therefore limiting x to greater than or equal to 3 prevents this, also, consideration should be given to the fraction

`(3)/(x + 2)`

if x has a value of -2 it causes the denominator of the fraction to be 0, the denominator should never be 0, by limiting x to greater than 3 to prevent the problem above you are already taking care of x not being able to be -2 since greater than 3 already excludes -2