Question

You owe $1,853.42 on a credit card with a limit of $3,000.00 at a rate of 15.5% APR. You pay $400.00 the first 2 months and then $200.00 until the bill is paid off. You pay the bill on the due date each month.​Can someone please help me

Answer 1

Count the number of months it takes to reach
`\( P_{\text{new}} \leq 0 \)`. This will be the number of months it takes to pay off the debt. By doing so, we get that It takes 5 months to pay off the debt.

To determine in how many months the debt will be paid off, we can use a spreadsheet or a loop to simulate the monthly payments and interest accumulation until the debt is fully paid.

Let's denote the following variables:

- P = principal amount (initial debt)

- r = monthly interest rate (APR / 12 / 100)

- n = number of months

- A = monthly payment

Given:

- P = $1,853.42

- r = 15.5\% / 12 / 100

- A = $400.00 for the first two months, then A = $200.00

The formula to calculate the remaining balance after each monthly payment is:

`\[ P_{\text{new}} = P_{\text{old}} * (1 + r) - A \]`

Here's the calculation:

1. For the first two months:

-
`\( P_{\text{new}} = P_{\text{old}} * (1 + r) - A \)`

-
`\( P_{\text{new}} = $1,853.42 * (1 + 0.155 / 12) - $400.00 \)`

-
`\( P_{\text{new}} = \text{New balance after the first payment} \)`

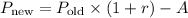
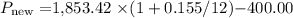
Repeat this for the second month using the new balance.

2. For the subsequent months:

-
`\( P_{\text{new}} = P_{\text{old}} * (1 + r) - $200.00 \)`

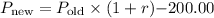
- Repeat this until
`\( P_{\text{new}} \leq 0 \)`

Count the number of months it takes to reach
`\( P_{\text{new}} \leq 0 \)`. This will be the number of months it takes to pay off the debt. By doing so, we get that It takes 5 months to pay off the debt.

The probable question may be: "You owe $1,853.42 on a credit card with a limit of $3,000.00 at a rate of 15.5% APR. You pay $400.00 the first 2 months and then $200.00 until the bill is paid off. You pay the bill on the due date each month.In how many months the debt is paid off?"