Question

Please help me solve Problem 21.2

Answer 1

__________________________________________________________

Hello! In this question, we are trying to find the maximum value of shear flow in the web of the wing spar. Note that we are trying to find this with a section that is 1 meter away from the free end of the beam.
__________________________________________________________

Step-by-step explanation:

In this problem, we know that:

• the web has a thickness of 2 mm.
• Fully effective in resisting direct stress

This information should be kept in mind and can help us solve our problem.

__________________________________________________________

Solve:

Let us begin to solve the problem.

Since we're analyzing the moment in one section, in this case, we can note this as "section 1", we can use this formula to determine the moment in this section:

`M_(1)=\frac{wl^2}2}`
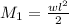
Whereas:

• w = distributed load (15 kN/m)
• l = length of beam (1 m)

Plug in the values into the equation and solve:

`M_(1)=\frac{15*1^2}2}=7.5\text{kN-m}`
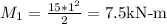
Now, let us find the moment of inertia of the beam in our 1st section. We'll use the formula:

`I_(xx)=(BD^3)/(12) +2Ah^2`

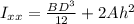
Whereas:

• B = width (2 mm)
• D = depth (300 mm)
• A = area (500 mm²)
• h = centroid of this section (150 mm)

Plug in the values into the equation and solve:

`I_(xx)=(2(300)^3)/(12) +2(500)(150)^2=2.7*10^7\:\text{mm}^4`
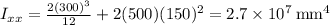
Now knowing our moment and inertia, we can solve our direct distress in the z direction of our flanges using the following formula:

`\sigma_(z,U) = -\sigma_(z,L)=(M_(1))/(I_(xx))y`
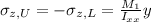
We know:

• 
  `M_(1)=7.5\text{kN-m}`
• 
  `I_(xx)=2.7*10^7\:\text{mm}^4`
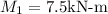
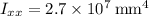
• y = 150mm

Plug the values into the equation and solve. (Note that unit conversion was done for M1):

`\sigma_(z,U) = -\sigma_(z,L)=\frac{7.5\text{kN-m}*((1000 N)/(1kN))((1000mm)/(1m) )}{2.7*10^7}(150mm)=-41.7\:\text{N/mm}^2`
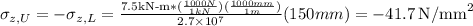
Since we now know what our direct distress is, we can find the bending moment resultant with the formula:

`P_(z,U)=\sigma_(z,U)* A`

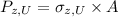
We know:

• 
  `\sigma_(z,U) = -\sigma_(z,L)=-41.7\:\text{N/mm}^2`
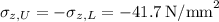
• A = 500 mm² (according to our wing spar given in our problem)

Plug in the values to our equation and solve:

`P_(z,U)=-41.7\:\text{N/mm}^2* 500\:mm^2=-20850\:N`
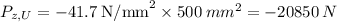
Now knowing our bending moment resultant, we can now find our flange load of the web section. Note that our flange load is uniformly distributed. We will use the formula:

`P_(U)=\sqrt{P_(z,U)^2+P_(y,U)^2}}`
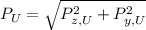
We know that:

• 
  `P_(z,U)^2= -20850\:N`
• 
  `P_(y,U)^2=0`

Plug in the values into the equation and solve:

`P_(U)=√((-20850)^2+0^2)}=20850\:N`
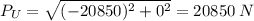
Please note that the answer we calculated above is our tension (T).

Let's now calculate our bending moment resultant using:

`P_(y,L)=P_(z,L)*\frac{\delta{y}^2}{\delta_(z)}`

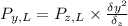
We know:

• 
  `P_(z,L)=-20850\:N`
• 
  `\delta{y}^2=100\:mm`
• 
  `\delta_(z)=1\:m`

Plug in the values and solve. To make things go faster, I included the unit conversion for our denominator value:

`P_(y,L)=-20850\:N*(100\:mm)/((1\:m*(1000\:mm)/(1\:m) ))=-2085\:kN=2085\:kN`
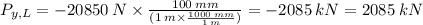
Please note that the above calculation would be our compression value.

Let's calculate our shear force in the web in our 1st section using a known relationship:

`S_(y)=-W*\delta_(z)+P_(y,L)`
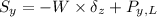
We know:

• W = 15 kN/m
• 
  `\delta_z=1\:m`
• 
  `P_(y,L)=2085\:N`

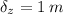
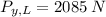
Plug in our known values and solve:

`S_(y)=-15*(1\:m*(1000\:mm)/(1\:m) )+2085=-12915\:N`

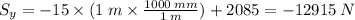
In order to figure out what our shear flow is (note that our shear flow is represented as q), we will use the relationship:

`q=(S_y)/(I_(xx)) [\int_(0)^(s)2(150-s)ds+500*((300)/(2) )]`

We know:

• 
  `S_(y)=-12915\:N = 12915\:N`
• 
  `I_(xx)=2.7*10^7\:mm`

Plugging in the values, we will get:

`q=(12915)/(2.7*10^7\:mm) [\int_(0)^(s)2(150-s)ds+500*((300)/(2) )]`

Simplify the equation:

`q=4.78*10^(-4) [\int_(0)^(s)(300-s)ds+75000]`
Integrate the equation:

`q=4.78*10^(-4) [\int_(0)^(s)(300-s)ds+75000]\\\\q=4.78*10^(-4) ((300s-(2s^2)/(2) +[0])+75000)\\\\q=4.78*10^(-4) ((300s-s^2 )+75000)`

We now have our equation for the shear flow. We know that the max value of shear flow will happen when s equals 150 mm, so let's plug in the value 150 mm into "s" in our "q" equation and solve:

`q=4.78*10^(-4) ((300(150)-150^2 )+75000)=\boxed{46.8\:N/mm}`

__________________________________________________________

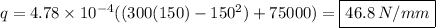
Answer:

The max value of shear flow in the web in the 1st section of the beam is:

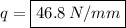
`q=\boxed{46.8\:N/mm}`

__________________________________________________________