Question

A 0.5 kg particle is moving in a circle of radius 2 meters according to the relation

θ = 5t^(3)+ 4t^(2) + 3t where θ is measured in radians and t in seconds.
(a) What is the translational speed of the particle at 4 seconds?
(b) What is the angular acceleration of the particle at 4 seconds?
(c) What is the net force on the particle at 4 seconds?

Answer 1

(a) 550 m/s

(b) 128 rad/s²

(c) 75625 N

Step-by-step explanation:

To address this problem, we'll break it down into its three components: translational speed, angular acceleration, and net force, all at a specific time of 4 seconds for a particle moving in circular motion.

Given angular position function:

`\theta (t) = 5t^3+ 4t^2 + 3t`

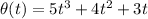
We are also given:

• m = 0.5 kg
• r = 2 m

`\hrulefill`

(a) Translational Speed at 4 seconds:
`\hrulefill`

To find the translational speed 'v' of the particle at t = 4 seconds, we first need to determine the angular velocity 'ω'. Angular velocity function 'ω(t)' is the derivative of the angular position function 'θ(t)' with respect to time 't':

`\Longrightarrow \theta (t) = 5t^3+ 4t^2 + 3t\\\\\\\\\Longrightarrow (d)/(dt)\left[ \theta (t) = 5t^3+ 4t^2 + 3t\right]\\\\\\\\\Longrightarrow (d)/(dt)\left[ \theta (t)\right] = (d)/(dt)\left[5t^3+ 4t^2 + 3t\right]\\\\\\\\ \therefore \omega (t)=15t^2+8t+3`

Now plug in t = 4:

`\Longrightarrow \omega (4)=15(4)^2+8(4)+3\\\\\\\\\therefore \omega (4) = 275 \text{ rad/s}`

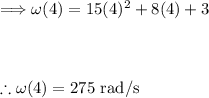
Now we can relate angular speed to translational speed using the formula 'v = rω'. Substitute in our values:

`\Longrightarrow v_t=(2 \text{ m})(275 \text{ rad/s}) \\\\\\\\\therefore v_t = \boxed{550 \text{ m/s}}`

Thus, the translational speed of the particle at t = 4 seconds is 550 m/s.

`\hrulefill`

(b) Angular Acceleration at 4 seconds:
`\hrulefill`

To find the angular acceleration, we need to find the angular acceleration function. The angular acceleration function 'α(t)' is the derivative of angular velocity function 'ω(t)' with respect to time t. Taking the derivative:

`\Longrightarrow \omega (t)=15t^2+8t+3\\\\\\\\\Longrightarrow (d)/(dt) \left[ \omega (t)=15t^2+8t+3\right]\\\\\\\\\Longrightarrow (d)/(dt) \left[ \omega (t) \right]=(d)/(dt) \left[15t^2+8t+3\right]\\\\\\\\\therefore \alpha (t)=30t+8`

Now plug in t = 4:

`\Longrightarrow \alpha (4)=30(4)+8\\\\\\\\\therefore \alpha (t) = \boxed{128 \text{ rad/s$^2$}}`

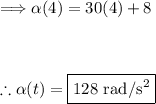
Thus, the angular acceleration of the particle at t = 4 seconds is 128 rad/s².

`\hrulefill`

(c) Net Force on the Particle at 4 seconds:
`\hrulefill`

The net force 'F' acting on an object in circular motion can be found using the formula F = ma_c, where 'm' is the mass of the particle and 'a_c' is the centripetal acceleration. The centripetal acceleration can be found using a_c = v²/r, where 'v' is the translational speed we calculated in part (a). Let's now calculate these values:

`\Longrightarrow F_{\text{net}}= (0.5 \text{ kg})\left(\frac{(550 \text{ m/s})^2}{2 \text{ m}}\right)\\\\\\\\\therefore F_{\text{net}}=\boxed{75625 \text{ N}}`

Thus, the net force on the particle at t=4 seconds is 75625 N.