Question

Given the following information, find the equation in vertex form, factored form and standard form.

1. Vertex (1, 4) Point (2, -1)
Vertex form
Standard form

Answer 1

Vertex:

`f(x)=-5(x-1)^2+4`

Standard:

`f(x)=-5x^2+10x-1`

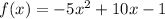
Factored:

This is unfactorable.

Explanation:

The parabola has a vertex at (1, 4) and it crosses a point at (2, -1).

We will start off with the vertex form, given by:

`f(x)=a(x-h)^2+k`

Where (h, k) is the vertex.

Therefore:

`f(x)=a(x-1)^2+4`

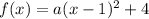
Since the function passes through (2, -1), f(x) = -1 when x = 2:

`-1=a(2-1)^2+4`

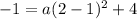
Solve for a:

`-5=a(1)\Rightarrow a =-5`

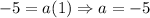
Therefore, vertex form is:

`f(x)=-5(x-1)^2+4`

To find the standard form, expand:

`f(x)=-5(x^2-2x+1)+4`

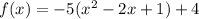
Distribute:

`f(x)=-5x^2+10x-5+4`

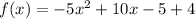
And simplify:

`f(x)=-5x^2+10x-1`

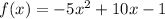
We can now factor. Which two values multiply to be 5 and add up to be 10?

Since this is no possible, the equation is unfactorable.