Question

A polynomial function has a root of -5 with multiplicity 3, a root of 1 with multiplicity 2, and a root of 3 with multiplicity 7. If the function has a negative leading coefficient and is of even degree, which statement about the graph is true?

A. The graph of the function is positive on (-infinity, -5)
B. The graph of the function is negative on (-5, 3)
C. The graph of the function is positive on (-infinity, 1)
D. The graph of the function is negative on (3, infinity).​

Answer 1

D

Explanation:

Let's first write the possible function described.

The roots are:

-5 with a multiplicity of 3.

1 with a multiplicity of 2.

And 3 with a multiplicity of 7.

And the leading coefficient is negative.

Therefore:

`f(x)=-a(x+5)^3(x-1)^2(x-3)^7`

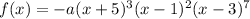
Where a is a positive value.

We want to know which statement is true about the graph.

First, since the second root is squared, it will always be positive. And since the leading coefficient is negative, our function is now negative.

So, we will only need to test the first and third root, as only they can alter the sign of our function.

Choice A)

(-∞, -5).

Pick any point within this interval. We can use -6 for simplicity. As stated previously, we only need to test the first and third root. We can ignore the exponents as well, since they do not alter signs. Therefore:

`(-6+5)(-6-3)=(-1)(-9)=9>0`

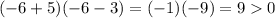
Since the result is positive, and our function is already negative, our function is negative for (-∞, -5).

A is not correct.

Choice B)

(-5, 3)

Choosing 0:

`(0+5)(0-3)=-15<0`

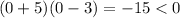
Negative times negative is positive. So, f(x) will be positive for (-5, 3).

B is not correct.

Choice C)

(-∞, 1).

Choosing 0, we can see that:

`(0+5)(0-3)=-3<0`

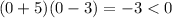
Negative times a negative is positive. So, it seems that C is correct.

However, notice that the domain (-∞, 1) contains two roots: x = -5 and x = 1.

In reality, we only tested (-5, 1). We have yet to test (-∞, -5). So, by using -6 again:

`(-6+5)(-6-3)=(-1)(-9)=9`

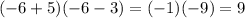
Positive times negative is negative.

So, f(x) is both positive and negative for (-∞, 1).

C is not correct.

Note: We did not need to double-check for B since it was already false.

Choice D)

(3, ∞)

This only has one root.

And using 4, we see that:

`(4+5)(4-3)=1>0`

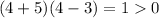
Positive times a negative will be negative.

Hence, f(x) will be negative for (3, ∞).

Choice D is the correct answer.