Question

E^y = (4x-x^3)/(x+2) rearrange to find x in terms of y

Answer 1

The solutions for x in terms of y are x = 2, x = -2, and
`x = -e^y`.

To solve the equation
`\(e^y = (4x - x^3)/(x + 2)\)` for x in terms of y, follow these steps:

Step 1: Clear the Fraction:

Multiply both sides of the equation by x + 2 to clear the fraction:

`\[ e^y(x + 2) = 4x - x^3 \]`

Step 2: Rearrange the Equation:

Expand the left side and move all terms to one side of the equation:

`\[ e^yx + 2e^y = 4x - x^3 \]`

Rearrange to get all terms on one side:

`\[ x^3 + e^yx - 4x + 2e^y = 0 \]`

Step 3: Factor the Equation:

Factor out common terms:

`\[ (x - 2)(x + 2)(x + e^y) = 0 \]`

Step 4: Solve for x:

Set each factor equal to zero and solve for x:

`x - 2 & = 0 \implies x = 2`

`x + 2 & = 0 \implies x = -2`

`x + e^y & = 0 \implies x = -e^y`

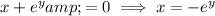
So, the solutions for x in terms of y are x = 2, x = -2, and
`x = -e^y`.