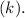The parabola
 models the height of a vertically launched object. The vertex, representing max height, is at (2, k), reached at 2 seconds.
models the height of a vertically launched object. The vertex, representing max height, is at (2, k), reached at 2 seconds.
Suppose an object is launched vertically, and its height,
 above the ground over time,
above the ground over time,
 , is modeled by the parabolic equation
, is modeled by the parabolic equation
 where
where
 is in meters and
is in meters and
 is in seconds. The given transformation indicates that the parabola narrows by a factor of 3, opens downward, and shifts right 2 units. In this context:
is in seconds. The given transformation indicates that the parabola narrows by a factor of 3, opens downward, and shifts right 2 units. In this context:
1. Vertex of the Parabola:
The vertex, representing the maximum height of the object, is at
 The rightward shift by 2 units places the vertex at
The rightward shift by 2 units places the vertex at
 and the downward opening is reflected in the negative coefficient,
and the downward opening is reflected in the negative coefficient,
 indicating the parabola opens downward.
indicating the parabola opens downward.
2. Time of Maximum Height:
The time at which the object reaches its maximum height corresponds to the
 -coordinate of the vertex. Therefore, the object reaches its peak at
-coordinate of the vertex. Therefore, the object reaches its peak at
 seconds.
seconds.
3. Initial Height:
The initial height of the object is given by the constant term \(k\). As it is not specified in the given information, the specific value of \(k\) would need to be provided to determine the initial height.
In summary, understanding the transformations applied to the original parabola allows us to analyze the object's motion, finding the vertex, time of maximum height, and, with additional information, the initial height of the launched object.
The probable question maybe:
What is the equation to model the height
 of an object launched vertically, considering the parabolic form
of an object launched vertically, considering the parabolic form
 ? Determine the vertex, time of peak height, and initial height
? Determine the vertex, time of peak height, and initial height