The equation √(5v) = v has two solutions, v = 0 and v = 5, after solving and verifying that they are not extraneous solutions. To solve, the equation is squared to eliminate the square root, set to zero, and then factored, yielding two potential solutions that need to be checked in the original equation.
When solving the equation involving the square root of a variable, such as square root of 5v = v, we have to be cautious about extraneous solutions.
These are solutions that, while they may emerge during the process of solving the equation, don't actually satisfy the original equation when we substitute them back in. Let's proceed to solve the given equation step by step.
To isolate the square root, square both sides of the equation:
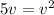
Now, rearrange the equation to set it to zero:
v² - 5v = 0
Factor out v:
v(v - 5) = 0
Our potential solutions are v = 0 and v = 5. However, we must check each one to ensure they are not extraneous. Substituting them back into the original equation:
√(5×0) = 0, which simplifies to 0 = 0. So, v = 0 is a valid solution.
√(5×5) = 5, which simplifies to √25 = 5. Since 5 = 5, v = 5 is also a valid solution.
Both solutions are valid and are not extraneous. Therefore, the solutions to the equation √(5v) = v are v = 0 and v = 5.