Question

Extraneous Solutions

Answer 1

The (x = -8) is an extraneous solution, and the valid solution is (x = 5).

To find extraneous solutions, solve the given equation for x and then check for values that lead to undefined or impossible expressions. Starting with
`\(x = √(40 - 3x)\)`:

1. Square both sides to eliminate the square root:
`\(x^2 = 40 - 3x\).`

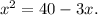
2. Rearrange to form a quadratic equation:
`\(x^2 + 3x - 40 = 0\).`

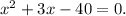
3. Factor the quadratic:
`\((x - 5)(x + 8) = 0\).`

4. Set each factor equal to zero: (x - 5 = 0) or (x + 8 = 0).

5. Solve for (x): (x = 5) or (x = -8).

Now, check for extraneous solutions by substituting these values back into the original equation.

Plugging (x = 5) yields a valid expression.

However, substituting (x = -8) results in taking the square root of a negative number, which is undefined in the real number system.

Therefore, (x = -8) is an extraneous solution, and the valid solution is (x = 5).

The probable question may be:

Extraneous Solutions

x=\sqrt{40-3x}