Question

Block B (of mass m) is initially at rest. Block A (of mass 3m) travels toward B with an initial speed v0 (vee nought) and collides in an inelastic collision. Given that all surfaces have negligible friction, determine the maximum height h reached by the

two blocks.

Answer 1

The maximum height reached by the two blocks is approximately 0.1147959 × v₀²

Step-by-step explanation:

The mass of block B = m

The mass of block A = 3·m

The initial velocity of block B, v₂ = 0 m/s

The initial velocity of block A, v₁ = v₀

The amount of friction between the blocks and the surface = Negligible friction

By the Law of conservation of linear momentum, we have;

Total initial momentum = Total final momentum

3·m·v₁ + m·v₂ = (3·m + m)·v₃ = 4·m·v₃

Plugging in the values for the velocities gives;

3·m × v₀ + m × 0 = (3·m + m)·v₃ = 4·m·v₃

∴ 3·m × v₀ = 4·m·v₃

`\therefore v_3 = (3)/(4) * v_0 = 0.75 * v_0`

The kinetic energy, K.E. of the combined blocks after the collision is given as follows;

K.E. = 1/2 × mass × v²

`\therefore K.E. = (1)/(2) * 4\cdot m * \left ((3)/(4) \cdot v_0 \right )^2 = (9)/(8) \cdot m\cdot v_0^2`

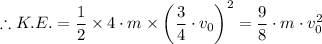
The potential energy, P.E., gained by the two blocks at maximum height = The kinetic energy, K.E., of the two blocks before moving vertically upwards

The potential energy, P.E. = m·g·h

Where;

m = The mass of the object at the given height

g = The acceleration due to gravity

h = The height at which the object of mass, 'm', is located

Therefore, for h = The maximum height reached by the two blocks, we have;

P.E. = K.E.

`m \cdot g \cdot h = (9)/(8) \cdot m\cdot v_0^2`

`h = ((9)/(8) \cdot m\cdot v_0^2)/(m \cdot g ) = (9)/(8) \cdot ( v_0^2)/( g ) = (9)/(8) \cdot ( v_0^2)/( 9.8) = (42)/(392) \cdot v_0^2 \approx 0.1147959 \cdot v_0^2`

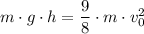
The maximum height reached by the two blocks, h ≈ 0.1147959·v₀².